项目地址:https://pypi.org/project/pycubelut/

本文会介绍以下内容:
- 什么是 LUT (Lookup Table)以及有什么作用。
- .cube 文件的结构。
- 通过 python 来读取图像做 LUT 映射,如何计算插值。
<1> 介绍
在我们开始之前,先对必要的背景知识做一些简单的铺垫。LUT 是 Lookup Table 的缩写,在图像处理方面,LUT 可以用来完成类似滤镜的效果,其原理本质上就是一个映射关系,输入颜色 (r, g, b),通过 LUT 去查找,得到一个新的颜色 (R, G, B),则完成了一次映射操作。
LUT 又分为 1D LUT 和 3D LUT,1D LUT 是指 R, G, B 三个分量互相不影响,都是独立映射,即存在 3 个映射  ,
,  ,
,  ,有如下关系存在。
,有如下关系存在。

而 3D LUT 则是存在一个映射关系  。可以这样想象一下方便理解,我们有一个三维的坐标系,长宽高的取值范围都是 1,长宽高可以表示为 RGB 三个分量的值,而这个坐标系围成的立方体中,填满了某种混合颜色的涂料,并且固化在里面。那么任意颜色
。可以这样想象一下方便理解,我们有一个三维的坐标系,长宽高的取值范围都是 1,长宽高可以表示为 RGB 三个分量的值,而这个坐标系围成的立方体中,填满了某种混合颜色的涂料,并且固化在里面。那么任意颜色  随便取一个值,即可以在这个坐标系中找到这样一个点,我们通过黑科技,把这个点对应的颜料取出来看一看,发现它的颜色是
随便取一个值,即可以在这个坐标系中找到这样一个点,我们通过黑科技,把这个点对应的颜料取出来看一看,发现它的颜色是  。这就完成了一次映射,这个立方体,就是我们的映射关系。
。这就完成了一次映射,这个立方体,就是我们的映射关系。
<2> .cube 文件
知道了 LUT 的原理,那么应该如何表示呢?由于输入颜色到输出颜色的映射是任意的,比如,你完全可以将黑色映射成白色,白色映射成红色,红色映射成黑色类似这样,所以它的功能比调节色相、饱和度、对比度、明暗更加强大。对于这样任意的映射,我们只能采用枚举法来枚举,或者称为采样。
大多数情况,我们的颜色值的取值范围都是 (0, 0, 0) 到 (255, 255, 255),如果要将这个映射完全存储起来,我们需要 255 * 255 * 255 条颜色信息与之对应,那么这个数据量是庞大的,并不利于传播与使用。因此我们使用采样+插值的方法,仅使用 32 * 32 * 32 来对映射信息做采样,在运行时,再做插值来还原中间缺失的信息。
Adobe 公司推出了 .cube 的文件格式,本质上是纯文本文件,其 Specification 在这里:cube-lut-specification-1.0.pdf。
下面展示该文件的一个片段:
#Created by: Adobe Photoshop Export Color Lookup Plugin
#Copyright: (C) Copyright 2017 RocketStock
TITLE "Sepia"
#LUT size
LUT_3D_SIZE 32
#data domain
DOMAIN_MIN 0.0 0.0 0.0
DOMAIN_MAX 1.0 1.0 1.0
#LUT data points
0.086273 0.086273 0.086273
0.098907 0.087311 0.086761
0.111694 0.088409 0.087250
0.124847 0.089630 0.087769
0.138275 0.090942 0.088348
0.151978 0.092285 0.088959
0.166077 0.093750 0.089600
0.180420 0.095245 0.090240
0.195160 0.096832 0.090912
0.210175 0.098541 0.091675
0.225311 0.100250 0.092377
0.240631 0.102081 0.093170
0.255951 0.103973 0.093994
0.271210 0.105927 0.094849
0.286560 0.107971 0.095734
0.301910 0.110077 0.096710
// 文件未完
值得注意的是,LUT_3D_SIZE 后面紧跟的数字为 N,是这个 LUT 的采样大小,上述文件中为 32,也就是说,此文件记录了 32 * 32 * 32 个颜色信息。
DOMAIN_MIN 指定了颜色空间的最小值,DOMAIN_MAX 指定了颜色空间的最大值,两个加在一起决定了颜色空间的范围。
再往下则由一堆数字构成,每行 3 个数字,分别表示了 RGB 的分量,每行是一个颜色值,此文件中,定义了 32 * 32 * 32 个颜色值(有这么多行数字)。
那么这堆数据如何使用呢?假设我们有任意颜色  ,首先我们要将颜色分量变换到
,首先我们要将颜色分量变换到 之间,然后,第
之间,然后,第  行就是我们要取的颜色,
行就是我们要取的颜色, 。
。
<3> 插值
回想一下颜色立方体的例子,在坐标空间中,任意一个点的坐标都是由三个  之间的数构成的,显然,它是连续的,但是当我们计算出映射的颜色 n 时,这个 n 是离散的,它只能是在
之间的数构成的,显然,它是连续的,但是当我们计算出映射的颜色 n 时,这个 n 是离散的,它只能是在  之间的整数。
之间的整数。
插值的计算方法是这样的:
对于任意颜色 ,我们转换到
,我们转换到  之间时,都需要保留它们的上界和下界。比如 r = 0.21(我随便乱写的值),那么
之间时,都需要保留它们的上界和下界。比如 r = 0.21(我随便乱写的值),那么  ,我们对 6.51 同时做向上和向下取整,得到两个数,6 和 7。同样的,我们对 green 和 blue 做一样的处理,总共可以得到 6 个数,分别记为:
,我们对 6.51 同时做向上和向下取整,得到两个数,6 和 7。同样的,我们对 green 和 blue 做一样的处理,总共可以得到 6 个数,分别记为: ,H 表示上界,high 嘛,L 表示下界,low 嘛。
,H 表示上界,high 嘛,L 表示下界,low 嘛。
这样,我们可以通过公式  ,得到两个 Index:
,得到两个 Index:


接着,使用这两个 index,可以在 LUT 表里面找到对应的两个颜色值记为 colorH 和 colorL:


这两个颜色,就是距离我们的  最近的两个离散的点,接下来,我们需要根据这两个点做插值计算。
最近的两个离散的点,接下来,我们需要根据这两个点做插值计算。
下图表示:在任意  时,我们只能得到离散的最靠近的
时,我们只能得到离散的最靠近的  和
和  。
。
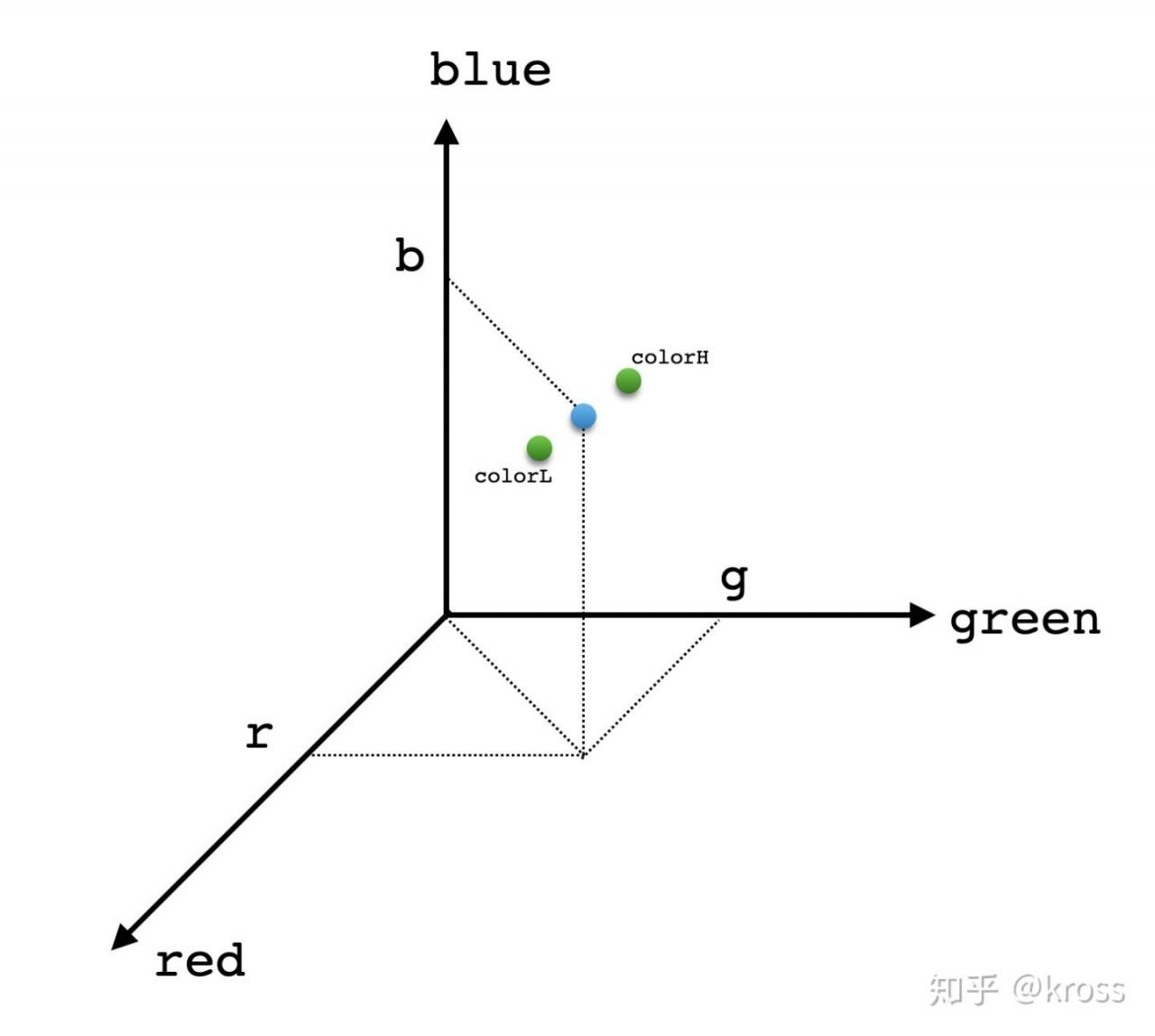
如何做插值呢?两个颜色相加直接除以2?当然这是一种方法,但未免太粗糙了,回想一下之前做的 r * 31 = 6.51,我们得到上界和下界 6 和 7,这里的意思不就是说,6.51 在 6 和 7 之间,小数部分(0.51)表示的倾向程度,如果是 6.21 ,说明这个数,更加倾向于 6,而 6.87 则是更加倾向于 7,因此我们可以用这个小数部分来做插值计算。
之前的步骤中,我们已经得到了归一化到[0,31]的颜色分量和两个颜色值:



我们现在定义一个计算表示取小数部分:

接着,我们就可以对三个颜色分量做插值了:



最终,我们就得到了映射后的颜色值了。
<4> Python 实现
最终代码实现于此,请自行下载查看:https://github.com/krossford/python-use-cube-lut-file-process-image
全文完。