https://hocassian.cn/wp-content/uploads/2020/05/122952c548739e1a83e932e530818a8ba0af214a.jpg
注:此文仅通过Python解析了一半试题,由于各种原因,本人不再更新,剩下的题目可以参考(@高玩梁 通过C++ 解析):

又到了秋……啊不对,是金九银十的秋季,与全体应届毕业生一样,同和君也开始要面临毕业出路的问题了。其中,很多公司的招聘流程都包括笔试和面试两座大山,而笔试的题目,尤其是算法编程题,分数占比相对较大,如果能在这些题目上发挥出色,想必会大大增加笔试通过的成功率~而且这些题目一般由对应公司命题,有的与公司文化密切相关,就比如我们接下来要解析的「哔哩哔哩2019秋招编程题」。
由于今年b站秋招已经过去,所以题目都被公布了出来(然鹅由于各种原因我于近期才向b站投递了简历……不知道人家还鸟不鸟我……),个人感觉其中有些题目很有意思,就开了这篇专栏打算和大家分享一下~
(试题资料来源:牛客网 https://www.nowcoder.com/test/16519291/summary)
*为方便理解,本文所涉代码统一采用Python语言编写

前有MHY「癞子算法」和「消消乐算法」(偏简单),后有WYYX「俄罗斯方块算法」和「球球大作战算法」(偏复杂),b站编程题的难度还是算中等的(我没有泄题啊!这些都是笔试完后企业自行公布的,我只是笔试的时候「在现场」罢了)。

第一题
22娘和33娘接到了小电视君的扭蛋任务:
一共有两台扭蛋机,编号分别为扭蛋机2号和扭蛋机3号,22娘使用扭蛋机2号,33娘使用扭蛋机3号。
扭蛋机都不需要投币,但有一项特殊能力:
扭蛋机2号:如果塞x(x范围为>=0正整数)个扭蛋进去,然后就可以扭到2x+1个
扭蛋机3号:如果塞x(x范围为>=0正整数)个扭蛋进去,然后就可以扭到2x+2个
22娘和33娘手中没有扭蛋,需要你帮她们设计一个方案,两人“轮流扭”(谁先开始不限,扭到的蛋可以交给对方使用),用“最少”的次数,使她们能够最后恰好扭到N个交给小电视君。
输入描述:输入一个正整数,表示小电视君需要的N个扭蛋。
输出描述:输出一个字符串,每个字符表示扭蛋机,字符只能包含"2"和"3"。
输入例子:10
输出例子:233

首先我们看他的测试用例,输入10,返回233,也就是22扭一次之后,33再扭两次。第一次啥都没有,22扭出来2*0+1=1个,然后将这一个交给33扭,得到2*1+2=4个,33再扭一次得到2*4+2=10个。这个时候我们就有一个大致的思路了,这道题需要从结果反推过程,这个时候有同学就会想了,题干中出现了「用“最少”的次数」这一句话,那么对于相同的「输入N」,会不会有不同的扭法呢?哎,那么这个时候,刷题积累的经验就派上用场了。我们再次看回「2x+1」、「2x+2」这两个表达式,相信有些聪明的朋友已经心领神会了哈。如果还是有点不清楚,上个图估计大家就秒懂了:
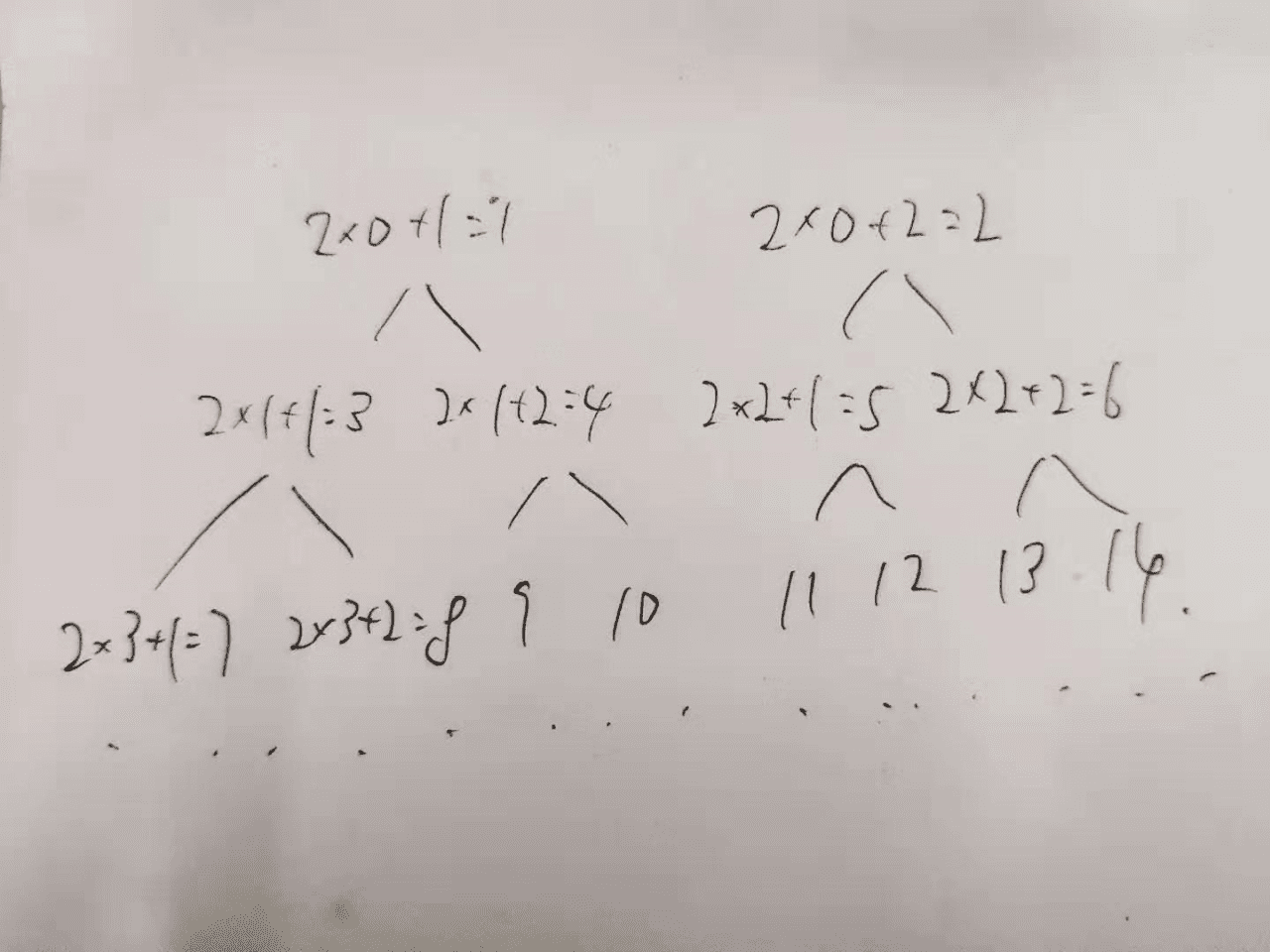
这不就是两颗有序的二叉树么?所有的N都对应一种独特的扭蛋顺序,也就是说不存在一个N对应多个扭法。了解了这一点之后,整个问题就好解答了,最简单的,我们用循环剥离的方法,列一个方程,把左边的移到右边去,一层层地判断输入N属于该二叉树的哪一个结点即可:
try:
while True:
N = int(input())
order = ''
while(N!=0):
if(N%2 == 0):
order = '3' + order
N = (N-2)/2
else:
order = '2' + order
N = (N-1)/2
print(order)
except:
pass高级一点的可以用递归:
try:
while True:
N = int(input())
order = ''
def egg(N, _order):
if(N == 0):
return _order
elif(N%2 == 0):
N = (N-2)/2
_order = egg (N, _order)+'3'
return _order
else:
N = (N-1)/2
_order = egg (N, _order)+'2'
return _order
order = egg(N, order)
print(order)
except:
pass这里留一个小小的问题给大家思考,为什么普通方法里插入’2’或’3’的方法是这样:order = '3' + order,而递归方法里就变成了这样:_order = egg (N, _order)+'3',恰好反过来了?


第二题
av394281 中,充满威严的蕾米莉亚大小姐因为触犯某条禁忌,被隙间妖怪八云紫(紫m……èi)按住头在键盘上滚动。
同样在弹幕里乱刷梗被紫姐姐做成罪袋的你被指派找到大小姐脸滚键盘打出的一行字中的第 `k` 个仅出现一次的字。
(为简化问题,大小姐没有滚出 ascii 字符集以外的字)
输入描述:每个输入都有若干行,每行的第一个数字为`k`,表示求第`k`个仅出现一次的字。然后间隔一个半角空格,之后直到行尾的所有字符表示大小姐滚出的字符串`S`。
输出描述:输出的每一行对应输入的每一行的答案,如果无解,输出字符串`Myon~` (请不要输出多余的空行),为了方便评测,如果答案存在且为c,请输出[c]
输入例子:
2 misakamikotodaisuki
3 !bakabaka~ bakabaka~ 1~2~9!
3 3.1415926535897932384626433832795028841971693993751o582097494459211451488946419191919l91919hmmhmmahhhhhhhhhh
7 www.bilibili.com/av170001
1 111
输出例子:
[d]
[9]
[l]
[7]
Myon~


看到这个题目,我们最直观的想法肯定是从头开始扫描这个字符串中的每个字符。当访问到某个字符时,拿这个字符和整个字符串中的每个字符相比较,如果没有发现重复的字符,则该字符就是只出现一次的字符,循环至输入k即可。如果字符串有n个字符,每个字符可能与后面的O(n)个字符相比较,因此这种思路的时间复杂度是O(n2)。
代码如下,其中count方法用于统计字符串里某个字符出现的次数,当该字符数为‘1’时即满足条件,存入备选栈stack:
try:
while True:
s = input().strip().split(' ',1)
n = int(s[0])
string = s[1]
stack = []
flag = 1
for i in string:
if (string.count(i)==1):
stack.append(i)
if len(stack)==n:
print('['+i+']')
flag = 0
break
if (flag == 1):
print("Myon~")
except:
pass我们运行一下试试看哈:
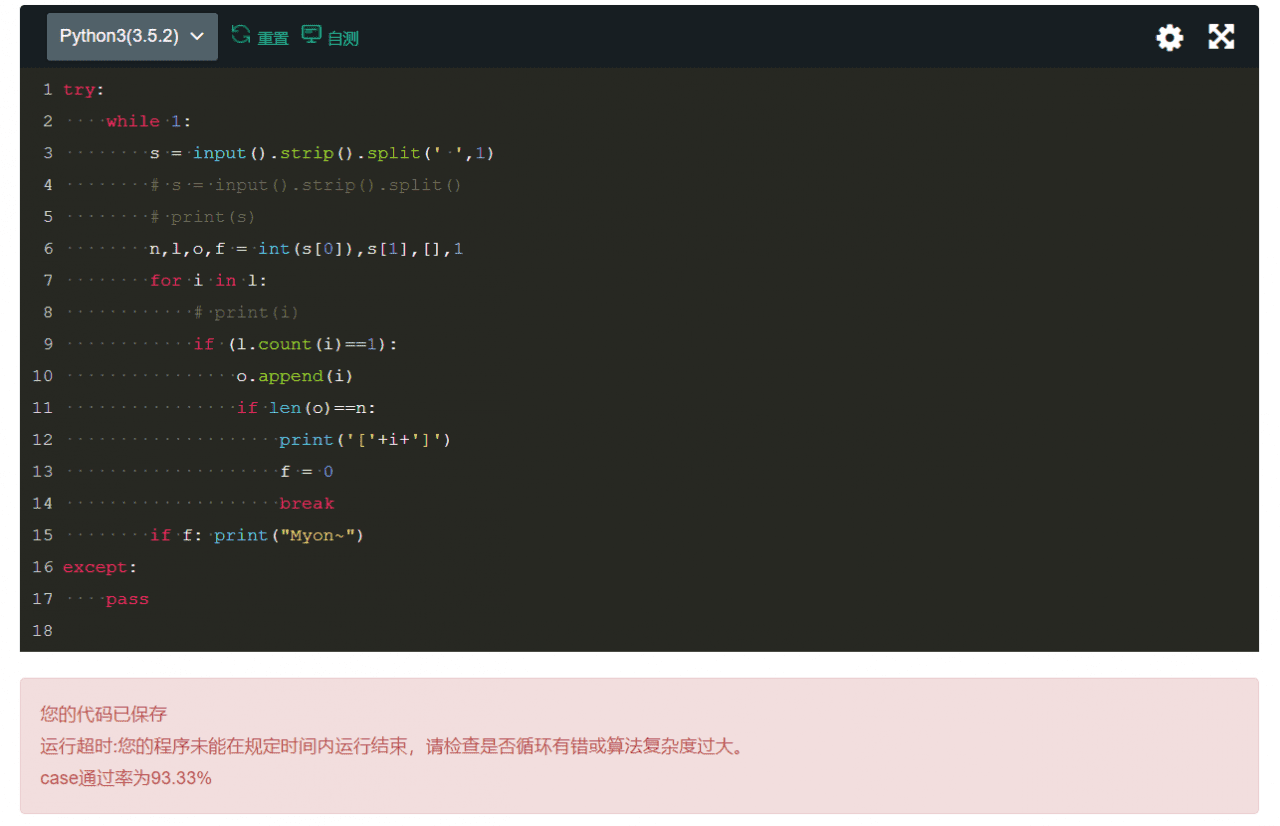
很可惜,超时了。所以这种情况下,我们要考虑用空间换时间,首先定义一个哈希表(外部空间),其键值(Key)是字符,而值(Value)是该字符出现的次数。同时我们还需要从头开始扫描字符串两次:第一次扫描字符串时,每扫描到一个字符就在哈希表的对应项中把次数加1。第二次扫描时,每扫描到一个字符就能从哈希表中得到该字符出现的次数。这样第k个只出现一次的字符就是符合要求的输出(时间复杂度O(n),满足题目限时要求)。
## r8i
## ,Br;; iaiXW
## WXr7X2aZr0r
## ;ZSX2ii7X;;
## ;XXiZWXaZ:;Zr
## S0ZX. ;aZS
## ,S27rX:,0X.S2:
## iXX:,X8M080@07;X7i
## .BZ8; rMW0Xr7BZ8BZ;:
## S2r:;ar:aXSZX2, S,;ri.
## 72;Br W0r7a8Sa;SZ:r.i.
## ,i0a@W0Z80XS7ZMWr,M.r
## i2S B0BMMMaZ; S.:
## :2 .8a08888;; .
## :i7X :X; SW020Wi ;; ,
## Z0aS:XX:r WWBZWWW .: ;
## 78Sr2i,X. MB@8MWB7.: 2:.
## Sr7BZS7 S@200@W0;.;80B;,i
## S2SaarM8aa2aZ82;B2,87
## .X;i7Xr rM@MWW8XX0XS7
## ,Z. ,72 @BM0@BM0;ZS r.
## a8. .Xa WW@B0@Z8MaX8; 2 , 7.
## iS:XS, XMZXWWBZZ0W;8S, 2 iZM.
## BM20 MW2;ZW@Z2@87B2XS8022:
## ,7iZaSWMWBSZ2MW0MM0WWZ, ;Z
## :Xi22 .aa0W@WWMWZ2XaWBi SBi
## i.. 8X X7ir; , ,2ZSS ,:
## ;a. .r@2, .0M7 .:i
## M@ @Mi
## MMi ,MBX
## WMM 8MM
##
## 紫 妹 保 佑 , 代 码 无 BUG
try:
while True:
s = input().strip().split(' ',1) # 输入
n = int(s[0])
hashTable = [] # 将字符串中存在的字符存进哈希表
_hashTable = {} # 用于计算每个字符重复次数的哈希数组
kind_of_char = 0 # 字符串中一共有多少种字符
for i in s[1]:
if i not in hashTable: # 每个字符只存一个进去,如果字符串中不止一个该字符,不存入
hashTable.append(i)
_hashTable[kind_of_char] = 1 # 挨个存入,与哈希表一一对应,初始值为'1'
kind_of_char += 1
else:
pos = hashTable.index(i) # 定位重复值在哈希表中的位置,并使与之对应的重复次数+1
_hashTable[pos] += 1
order = [] # 把只出现过一次的字符合并为新的列表
target = 0 # 共有多少只出现过一次的字符
for k in range(kind_of_char):
if(_hashTable[k] == 1):
order.append(hashTable[k])
target += 1
if(target == 0): # 如果根本没有只出现过一次的字符,直接给flag赋0
flag = 0
for j in range(target):
if(j == (n-1)): # 如果输入的n在只出现过一次的字符的数量之内,说明可以找到指定的值,即答
print('['+str(order[j])+']')
flag = 1
break
else: # 在限定范围以外,比如5 abcd,最末只出现过一次的字符为d,位置为4,不存在位置为5的符合条件的值,flag赋0
flag = 0
if(flag == 0):
print("Myon~") # MyonMyonMyon!
except:
pass
有小伙伴说用map做哈希映射表,这个方案更好,欢迎大牛补充代码~

第三题
给定一个合法的表达式字符串,其中只包含非负整数、加法、减法以及乘法符号(不会有括号),例如7+3*4*5+2+4-3-1,请写程序计算该表达式的结果并输出;
输入描述:输入有多行,每行是一个表达式,输入以END作为结束。
输出描述:每行表达式的计算结果。
输入例子:7+3*4*5+2+4-3-1
2-3*1
END
输出例子:69
-1

什么?python四则运算???直接exec完事!!!
while True:
i = input()
if i == "END":
break
exec('print('+i+')')额,好像有同学开始吐槽我投机取巧了:人家明明考的是输入表达式求值,你却直接转化一下丢给编译器?极客精神去哪里了?
好吧,那就自我挽尊一下吧(捂脸)。如果正常用C语言来解的话,我想起了之前学过的一个知识点:中缀表达式求值。可以看到标准的运算流程是十分复杂的,毕竟其中引入了诸多运算符,而不同的运算符的优先级也不同。
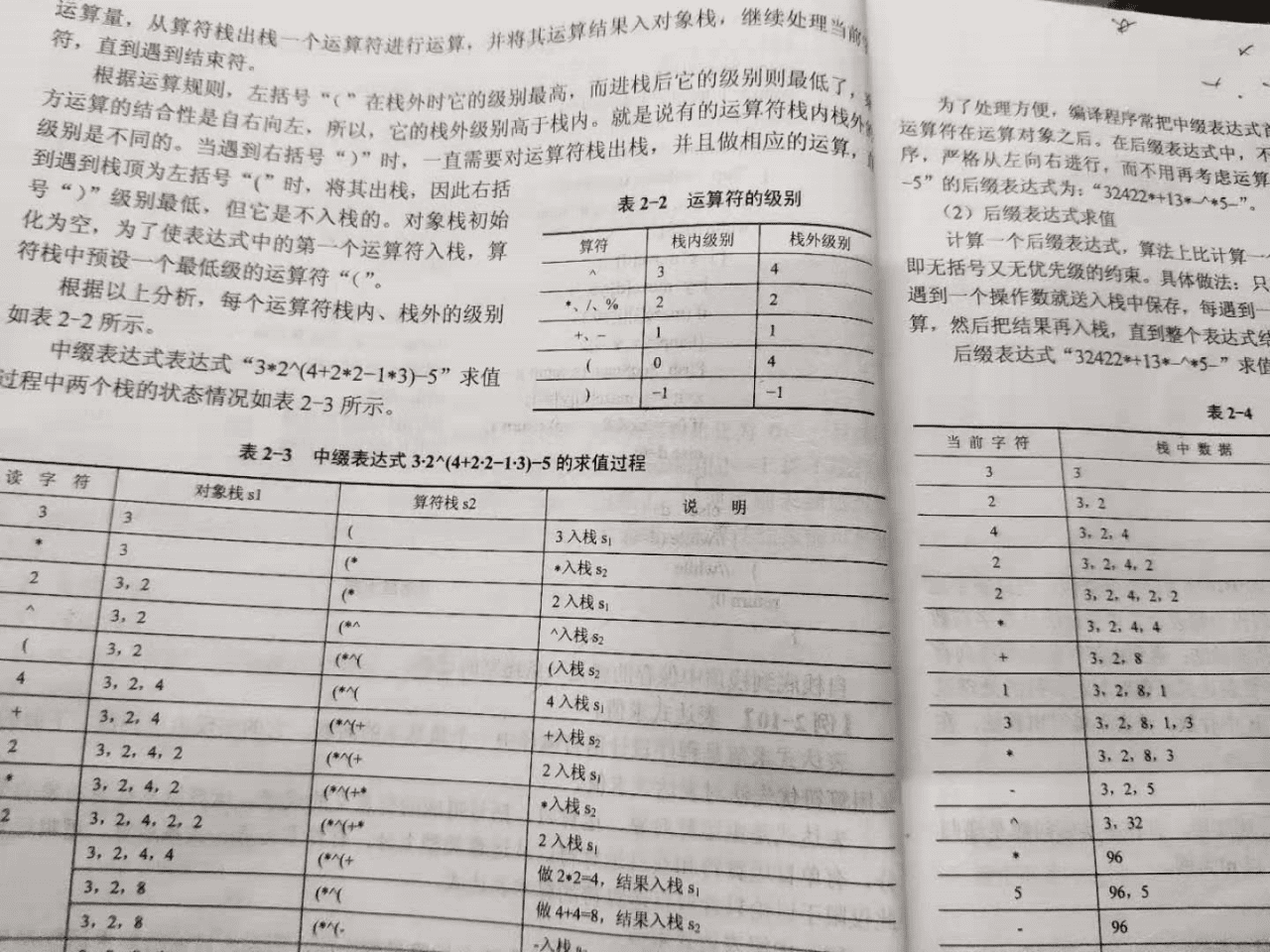
相比之下,这到测试题就简单了很多,只有加减和乘法这两个运算级别(甚至连除法都没有),这样一来,我们只需要考虑遇到’*’先计算,再计算‘+-’。老办法,还是出入栈算法(其实更应该称作一种思路),将依次判断输入的字符是数字还是运算符,接着入栈,以不同的优先级提取出栈运算后再入栈,最后得出结果。
def cal(exp):
num = 0
op = ''
while num < len(exp):
if exp[num].isdigit():
temp = ""
while num < len(exp) and exp[num].isdigit():
temp += exp[num]
num += 1
push_stack(int(temp), op)
else:
op = exp[num]
num += 1
def push_stack(value, op):
if op == "+" or op == "":
stack.append(value)
elif op == "-":
stack.append(value*(-1))
elif op == "*":
stack[-1] *= value
while True:
stack = []
exp = input()
if exp == "END":
break
else:
cal(exp)
print(sum(stack))
更高级的还可以选择递归,由于时间关系我就不自己写了,贴上大牛的代码以供参考。


第四题
小A参加了一个n人的活动,每个人都有一个唯一编号i(i>=0 & i<n),其中m对相互认识,在活动中两个人可以通过互相都认识的一个人介绍认识。现在问活动结束后,小A最多会认识多少人?
输入描述:
第一行聚会的人数:n(n>=3 & n<10000);
第二行小A的编号: ai(ai >= 0 & ai < n);
第三互相认识的数目: m(m>=1 & m
< n(n-1)/2);
第4到m+3行为互相认识的对,以','分割的编号。
输出描述:输出小A最多会新认识的多少人?
输入例子:7
5
6
1,0
3,1
4,1
5,3
6,1
6,5
输出例子:3

这道题我最开始做的时候超时了,且通过率只有26%,但总体方法应该没用错,属于并查集算法,先把n个人视为独立的个体,依次输入人物关系时进行连接,认识的人共用一个数字,即分组;最后根据小A编号查找他那一组一共有多少人,用这个数减去曾经就认识的人,就是答案。
这是第一次提交的时候发现的问题,该代码无法对组与组之间的值做连接,所以会发生以下这种错误:

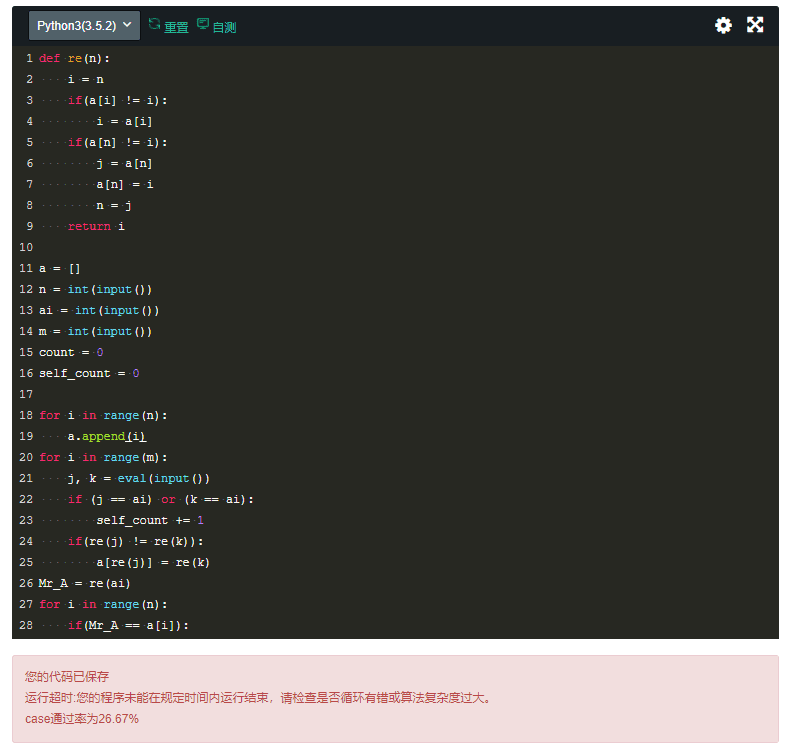
所以我打算直接用递归,遇到节点就判断当前节点的父节点是否为根节点,如果不是根节点,就将自己的父节点设置为根节点,最后返回到自己的父节点。
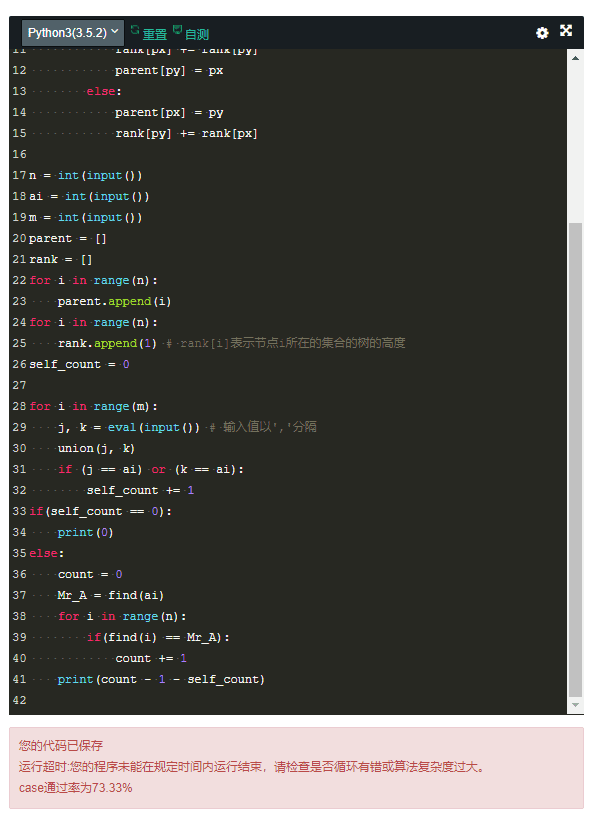
虽然最终结果只有73.33%,但思路已经理清晰了。大概是Python效率不高,需要的运算时间比较多。当然,也希望有大佬能提供效率更高的算法~
def find(x):
if(parent[x] != x): # 判断当前节点的父节点是否为根节点,如果不是根节点,就将自己的父节点设置为根节点,最后返回到自己的父节点
parent[x] = find(parent[x])
return parent[x]
def union(x, y): # 优化树结构
px, py = find(x), find(y)
if(px != py): # 通过访问rank[px]和rank[py]来比较两棵树的高度,将高度较小的那棵连到高度较高的那棵上。
if rank[px] >= rank[py]:
rank[px] += rank[py]
parent[py] = px
else:
parent[px] = py
rank[py] += rank[px]
n = int(input())
ai = int(input())
m = int(input())
parent = []
rank = []
for i in range(n):
parent.append(i) # 初始化,所有节点独立
for i in range(n):
rank.append(1) # rank[i]表示节点i所在的集合的树的高度
self_count = 0
for i in range(m):
j, k = eval(input()) # 输入值以','分隔
union(j, k)
if (j == ai) or (k == ai): # 排除已经认识的人
self_count += 1
count = 0
Mr_A = find(ai)
for i in range(n): # 遍历以找出包含小A的节点
if(find(i) == Mr_A):
count += 1
print(count - 1 - self_count)

第五题
金闪闪死后,红A拿到了王之财宝,里面有n个武器,长度各不相同。红A发现,拿其中三件武器首尾相接,组成一个三角形,进行召唤仪式,就可以召唤出一个山寨金闪闪。(例如,三件武器长度为10、15、20,可以召唤成功。若长度为10、11、30,首尾相接无法组成三角形,召唤失败。)红A于是开了一个金闪闪专卖店。他把王之财宝排成一排,每个客人会随机抽取到一个区间[l,r],客人可以选取区间里的三件武器进行召唤(客人都很聪慧,如果能找出来合适的武器,一定不会放过)。召唤结束后,客人要把武器原样放回去。m个客人光顾以后,红A害怕过多的金闪闪愉悦太多男人,于是找到了你,希望你帮他统计出有多少山寨金闪闪被召唤出来。
输入描述:
第一行武器数量:n <= 1*10^7
第二行空格分隔的n个int,表示每件武器的长度。
第三行顾客数量:m <= 1*10^6
后面m行,每行两个int l,r,表示每个客人被分配到的区间。(l<r)
输出描述:山寨金闪闪数量。
输入:
5
1 10 100 95 101
4
1 3
2 4
2 5
3 5
输出:3

首先要吐槽一下,金闪闪♂愉悦太多男人是个什么鬼啦!这就是你降低出货率的理由吗?
咳咳,进入正题,首先所有武器放置的顺序是无序的,但顾客从区间中取出能组成三角形的三把武器,是需要排序的,毕竟「客人都很聪慧」。要使两边边长的和大于第三边,降序或升序排好后显然更容易选择合适的召唤,数组的第i项和第i+1项相加,与i+2相比,一旦符合条件即为召唤成功。
所以代码呼之欲出:
n = int(input())
Gate_of_Babylon = list(map(int,input().split()))
m = int(input())
sum = 0
for j in range(m):
interval =input().split()
l = int(interval[0])
r = int(interval[1])
num = Gate_of_Babylon[l+1:r]
num.sort()
for i in range(0,len(num)-2):
if num[i]+num[i+1]>num[i+2]:
sum+=1
break
print(sum)检测不通过的提示也呼之欲出:
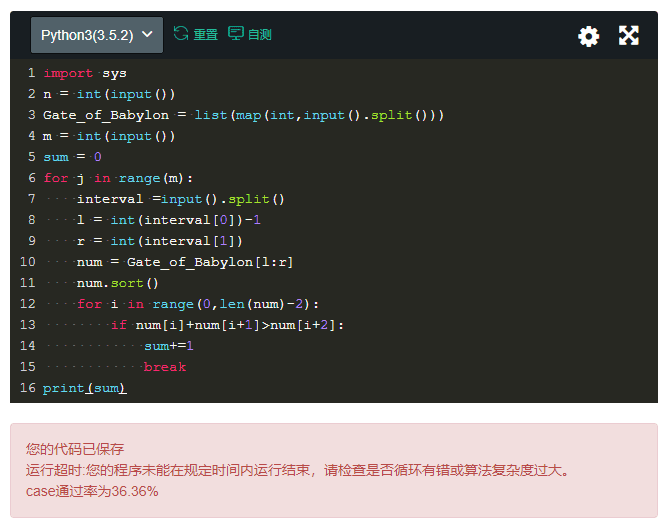
让我们看看时间复杂度爆炸的原因在哪里——
「第一行武器数量:n <= 1*10^7」
也就是说存在给这么多数字排序、两两相加并与后一位比较的情况?!难怪炸了。
所以这个时候,我们需要考虑一种能够简化运算的处理办法。一般来说,普通人做到这个地步已经很不错了,基本没法再优化了(毕竟实际生产环境中其实没多少特别长的用例),但我们是谁?我们可是面临「毕业即失业」警告的应届毕业生啊!不再优化优化,能被考官看上么?再说了,咱得有极客精神!
让我们再次回到题干,注意「第二行空格分隔的n个int,表示每件武器的长度」这一行,也就是说武器长度最长不超过2147483647,即int的最大赋值。那么,在[0,2147483647]的范围内,存不存在一个能使顾客刚好无法召唤金闪闪(排序后第i项和第i+1项相加小于第i+2项)的序列呢?这个序列最多能容纳多长的数组呢?
要达到这个目的,举例来说情况有这些:
1,1,2,3,5,8,13,21……
2,2,4,6,10,16,26……
3,3,6,9,15,21,36……
很明显第一条序列中的数字会多于2、3条的,而这条序列,似乎有点眼熟?

等等,好像拿错图了……
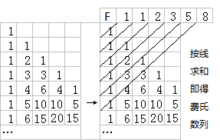
对,应该是这个,费氏数列。这个数列从第3项开始,每一项都等于前两项之和。所以我们得再写一个递归的代码,求出最长序列的长度:
def recur_fibo(n):
if n <= 1:
return n
else:
return(recur_fibo(n-1) + recur_fibo(n-2))
max = int(input("结果小于输入值的最大长度:"))
i = 0
while(max >= recur_fibo(i)):
i += 1
print(i)可能python+递归真的效率太低,电脑跑了5分钟愣是没跑出来……所以还是回到梦开始的地方,试试C语言吧……
#include<stdio.h>
int main(){
long long a=0,b=1,c=0,i,input;
scanf("%lld",&input);
for(i=2;c<input;i++){
c=a+b; //根据前面2项计算新的一项
printf("%lld %lldn",i,c); //输出一项
a=b; //为下一项计算作准备
b=c;
}
return 0;
}
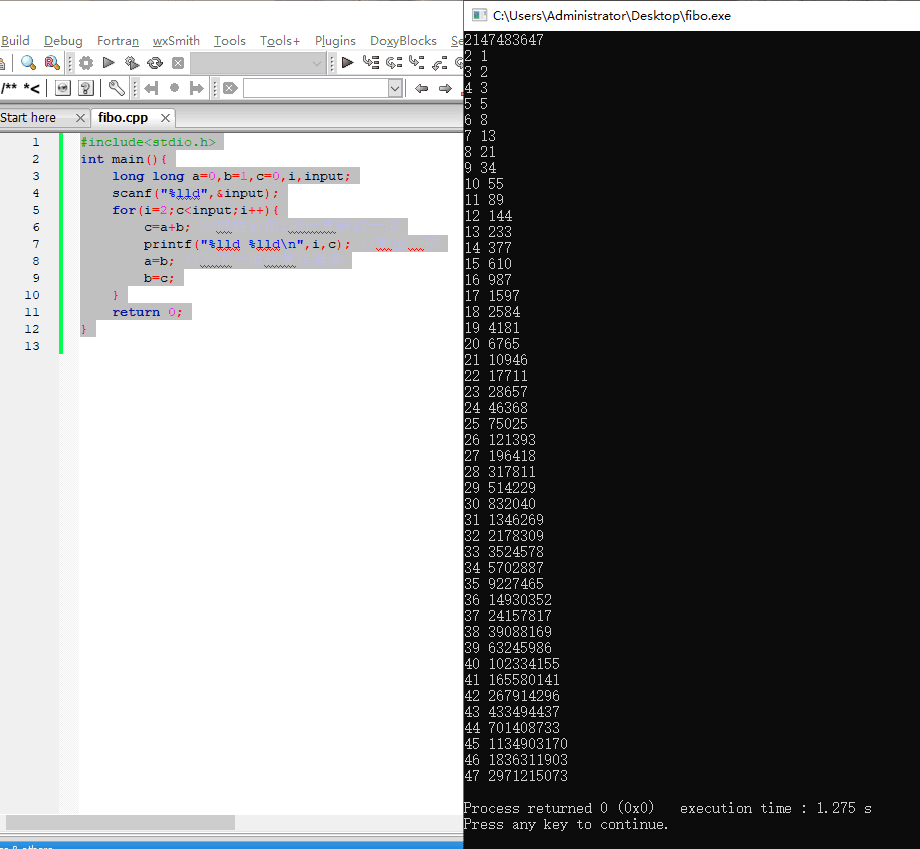
也就是说,只要在给出的区间长度较大的,一定能构成三角形,而对于那些区间长度小于47的,则可以存下来排序后逐项计算并判断。
最终修改代码为:
import sys
n = int(input())
Gate_of_Babylon = list(map(int,input().split()))
m = int(input())
sum = 0
for j in range(m):
interval =input().split()
l = int(interval[0])-1
r = int(interval[1])
if(r-l>=47):
sum+=1
else:
num = Gate_of_Babylon[l:r]
num.sort()
for i in range(0,len(num)-2):
if num[i]+num[i+1]>num[i+2]:
sum+=1
break
print(sum)

第六题
如果version1 > version2 返回1,如果 version1 < version2 返回-1,不然返回0.
输入的version字符串非空,只包含数字和字符.。.字符不代表通常意义上的小数点,只是用来区分数字序列。例如字符串2.5并不代表二点五,只是代表版本是第一级版本号是2,第二级版本号是5.
输入描述:
两个字符串,用空格分割。
每个字符串为一个version字符串,非空,只包含数字和字符.
输出描述:只能输出1, -1,或0
输入例子:0.1 1.1
输出例子:-1
备注:version1和version2的长度不超过1000,由小数点'.'分隔的每个数字不超过256。

这个就简单了,根据'.'分割输入的字符串,然后逐一对比大小:
def compare(a, b):
for i in range(min(len(a), len(b))):
if(a[i] < b[i]):
print('-1')
return
elif(a[i] > b[i]):
print('1')
return
if(len(a) == len(b)):
print('0')
else:
if(len(a) < len(b)):
print('-1')
else:
print('1')
return
version_input = input().split()
a, b = list(map(int, version_input[0].split('.'))), list(map(int, version_input[1].split('.')))
compare(a, b)然后才发现有更简单的方法:

还有更简单的:


第七题
猛兽侠中精灵鼠在利剑飞船的追逐下逃到一个n*n的建筑群中,精灵鼠从(0,0)的位置进入建筑群,建筑群的出口位置为(n-1,n-1),建筑群的每个位置都有阻碍,每个位置上都会相当于给了精灵鼠一个固定值减速,因为精灵鼠正在逃命所以不能回头只能向前或者向下逃跑,现在问精灵鼠最少在减速多少的情况下逃出迷宫?
输入描述:
第一行迷宫的大小: n >=2 & n <= 10000;
第2到n+1行,每行输入为以','分割的该位置的减速,减速f >=1 & f < 10。
输出描述:精灵鼠从入口到出口的最少减少速度?
输入例子:3
5,5,7
6,7,8
2,2,4
输出例子:19


这应该算是比较经典的动态规划问题了,只需要再多设置一个加权数组存储每个元素的加权值即可,详细说明已在注释中标出:
n = int(input())
# 初始化二维数组
maze, dp = [[0]*n for i in range(n)], [[0]*n for i in range(n)]
# 输入数字
for i in range(n):
maze_x = list(map(int, input().split(',')))
for j in range(n):
maze[i][j] = maze_x[j]
# 把第一个值赋给加权数组
dp[0][0] = maze[0][0]
for i in range(n-1):
# 首行的加权值
dp[0][i+1] = dp[0][i] + maze[0][i+1]
# 首列的加权值
dp[i+1][0] = dp[i][0] + maze[i+1][0]
# 中间项的加权值
for i in range(n-1):
for j in range(n-1):
# 某中间元素的加权值等于其min(上边,左边)
dp[i+1][j+1] = min(dp[i][j+1], dp[i+1][j]) + maze[i+1][j+1]
# dp最末端的值即为最小路径
# print(dp)
print(dp[-1][-1])
来看看大佬的代码,这位仁兄好像直接把原输入数组当成加权数组使用了:

OK,那么我们今天就分享到这里吧,剩下7道题感觉难度有所增加,就放到下一篇文章再分享吧。不得不说,这套题覆盖的知识点挺广,从数据结构到算法,基本每道题包含一两种算法,可能对于老手来说很简单,但对于我们这些学生来说,不好好复习一下以前算法课学过的内容,确实做不出来……

那么,感谢大家的阅读,希望这一点微不足道的分享能让你有所收获,祝福和我一样,同是应届毕业生的你,能赶上金九银十的招聘浪潮,找到合适自己的工作~

https://www.bilibili.com/read/cv3765805编程, 算法, 解析, 数据结构, 笔试题, Python, b站